Jensen's inequality

Jensens's inequality is a probabilistic inequality that concerns the expected value of convex and concave transformations of a random variable.

Table of contents

Convex and concave functions
Statement
Example
Important applications
Other inequalities
Solved exercises
1. Exercise 1
2. Exercise 2

Convex and concave functions

Jensen's inequality applies to convex and concave functions.

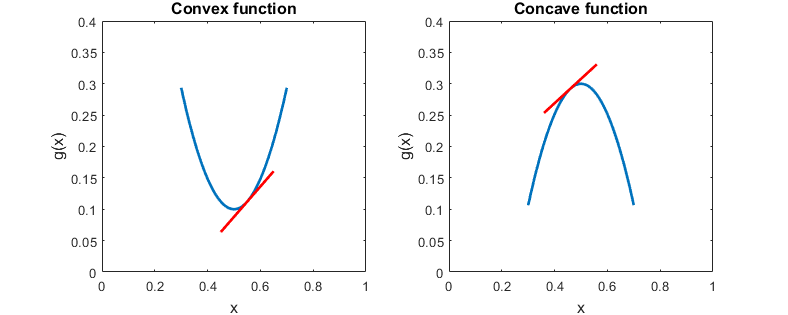
Property of convex and concave function that is needed to understand Jensen's inequalities.

The properties of these functions that are relevant for understanding the proof of the inequality are:

the tangents of a convex function lie entirely below its graph;
the tangents of a concave function lie entirely above its graph.

Also remember that a differentiable function is:

(strictly) convex if its second derivative is (strictly) positive;
(strictly) concave if its second derivative is (strictly) negative.

Statement

The following is a formal statement of the inequality.

Proposition Let be an integrable random variable. Let be a convex function such thatis also integrable. Then, the following inequality, called Jensen's inequality, holds:

Proof

A function is convex if, for any point $x_{0}$ the graph of lies entirely above its tangent at the point $x_{0}$ :where is the slope of the tangent. Setting and , the inequality becomesBy taking the expected value of both sides of the inequality and using the fact that the expected value operator preserves inequalities, we obtain [eq7]

If the function is strictly convex and is not almost surely constant, then we have a strict inequality:

Proof

A function is strictly convex if, for any point $x_{0}$ the graph of lies entirely above its tangent at the point $x_{0}$ (and strictly so for points different from $x_{0}$ ):where is the slope of the tangent. Setting and , the inequality becomesand, of course, when . Taking the expected value of both sides of the inequality and using the fact that the expected value operator preserves inequalities, we obtain [eq14] where the first inequality is strict because we have assumed that is not almost surely constant and therefore the eventdoes not have probability .

If the function is concave, then

Proof

If is concave, then is convex and by Jensen's inequality:Multiplying both sides by and using the linearity of the expected value we obtain the result.

If the function is strictly concave and is not almost surely constant, then

Proof

Similar to previous proof.

Example

Suppose that a strictly positive random variable has expected valueand it is not constant with probability one.

What can we say about the expected value of , by using Jensen's inequality?

The natural logarithm is a strictly concave function because its second derivative [eq21] is strictly negative on its domain of definition.

As a consequence, by Jensen's inequality, we have

Therefore, has a strictly negative expected value.

Important applications

Jensen's inequality has many applications in statistics. Two important ones are in the proofs of:

Other inequalities

If you like this page, StatLect has other pages on probabilistic inequalities:

Solved exercises

Below you can find some exercises with explained solutions.

Exercise 1

Let be a random variable having finite mean and variance $sigma ^{2}>0$ .

Use Jensen's inequality to find a bound on the expected value of $X^{2}$ .

Solution

The function we need to study isIt has first derivativeand second derivative [eq26] The second derivative is strictly positive on the domain of definition of the function. Therefore, the function is strictly convex. Furthermore, is not almost surely constant because it has strictly positive variance. Hence, by Jensen's inequality:Thus, the bound is

Exercise 2

Let be a positive integrable random variable.

Find a bound on the mean of .

Solution

The function we need to study isIt has first derivativeand second derivative [eq31] The second derivative is negative on the domain of definition of the function. Therefore, the function is concave and Jensen's inequality gives:Thus, the bound is

How to cite

Please cite as:

Taboga, Marco (2021). "Jensen's inequality", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-probability/Jensen-inequality.