Learn the basics of asymptotic theory: how sequences of random variables and random vectors are characterized, how their convergence is defined, what conditions guarantee their convergence.
Generalizes the concepts introduced in the lecture on sequences of random variables
Various definitions, including IID, stationary, ergodic, mixing
Convergence of almost all the sequences of real numbers obtained by fixing a sample point
Convergence of all the sequences of real numbers obtained by fixing a sample point
Convergence to zero of the mean-square distance between the limit and the terms of the sequence
Convergence to zero of the probability of being far from the limit
Relations among modes of convergence
Relations among different concepts of stochastic convergence
Convergence of the distribution functions of the terms of the sequence to the distribution function of the limit
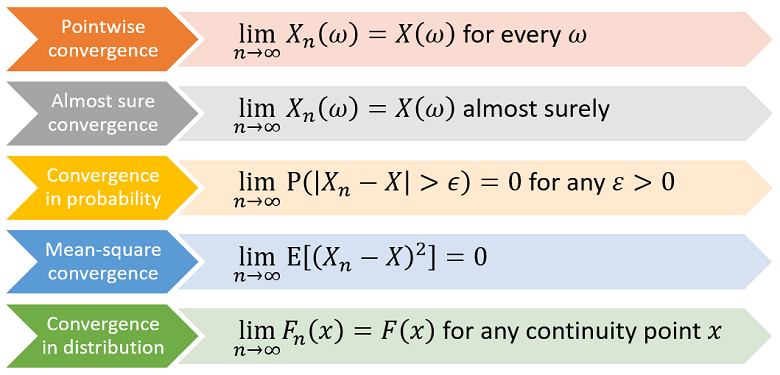
Conditions guaranteeing that the sample average converges to a normal distribution
Conditions guaranteeing that the sample average converges to the true mean
An important application of the Continuous Mapping theorem
Stochastic convergence is preserved by continuous transformations
A method used to derive the asymptotic distribution of a function of an asymptotically normal sequence
How to use the empirical distribution to approximate features of the original distribution
The distribution function of the discrete distribution of a sample of observations
A method used to reduce the variance of Monte Carlo estimates
Application of the plug-in principle to computer-generated samples
Most of the learning materials found on this website are now available in a traditional textbook format.