Importance sampling is a variance reduction technique used to reduce the variance of the approximation error made when approximating an expected value with Monte Carlo integration.
Importance sampling is based on a simple technique that allows to compute expected values in many different but equivalent ways.
The next proposition shows how the technique works for discrete random vectors.
Proposition
Let
be a
discrete random vector with support
and joint probability
mass function
.
Let
be a function
.
Let
be another
discrete random vector
with joint probability mass function
and such that
whenever
.
Then,
![[eq6]](/images/importance-sampling__13.png)
This is obtained as
follows:![[eq7]](/images/importance-sampling__14.png)
An almost identical propositon holds for continuous random vectors.
Proposition
Let
be a continuous
random vector with support
and joint probability
density function
.
Let
be a function
.
Let
be another continuous random vector
with joint probability density function
and such that
whenever
.
Then,
![[eq13]](/images/importance-sampling__26.png)
This is obtained as
follows:![[eq14]](/images/importance-sampling__27.png)
where
we have
usedas
a shorthand for the multiple integral over the coordinates of
.
Suppose we need to compute the expected
value
of a function of a random vector
by Monte Carlo integration.
The standard way to proceed is to use a computer-generated sample
,...,
of realizations of
independent random vectors
,...,
having the same distribution as
,
and use the sample mean
to
approximate the expected value.
Thanks to the propositions in the previous section, we can compute an
alternative Monte Carlo approximation of
by extracting
independent draws
from the distribution of another random vector
(in what follows we assume that it is discrete, but everything we say applies
also to continuous vectors) and by using the sample
mean![[eq20]](/images/importance-sampling__43.png)
as
an approximation. This technique is called importance
sampling.
The reason why importance sampling is used is that
can often be chosen in such a way that the variance of the approximation error
is much smaller than the variance of the standard Monte Carlo approximation.
In the case of the standard Monte Carlo approximation, the variance of the
approximation error
iswhile,
in the case of importance sampling, the variance of the approximation error
is
In the standard case, the approximation
error
isand
its variance
is![[eq24]](/images/importance-sampling__48.png)
In
the case of importance sampling, we
have![[eq25]](/images/importance-sampling__49.png)
Ideally, we would like to be able to choose
in such a a way that
is
a constant, which would imply that the variance of the approximation error is
zero.
The next propostion shows when this ideal situation is achievable.
Proposition
If
for any
,
thenwhen
has joint probability mass
function
The ratio
is
constant if the proportionality
conditionholds.
By imposing that
be a legitimate probability density function, we
get![[eq33]](/images/importance-sampling__60.png)
or
Of course, the denominator
is unknown (otherwise we would not be discussing how to compute a Monte Carlo
approximation for it), so that it is not feasible to achieve the optimal
choice for
.
However, the formula for the probability mass function of the optimal
gives us some indications about the choice of
.
In particular, the
formulatells
us that the probability mass function of
should place more mass where the product between the probability mass function
of
and the value of the function
is larger. In other words, the probability mass function of
should be tilted so as to give more weight to the values of
for which
is larger.
In the previous sections we have seen that importance sampling consists in
computing an alternative Monte Carlo approximation of
by extracting
independent draws
from the distribution of another random vector
and by using the sample
meanas
an approximation. We have also seen that this approximation has small variance
when the probability mass function of
puts more mass than the probability mass function of
on the values of
for which
is larger. This makes intuitive sense: if
is larger at some points, then we should try to sample
more frequently at those "important" points (in order to be more accurate
about the value of
at those points); then, when we average our samples, we should take into
account the fact that we over-sampled the important points by weighting them
down with the weights
which
are smaller than
when
is smaller than
.
Let us now illustrate importance sampling with an example.
Suppose
has a standard normal distribution (i.e., with mean
and standard deviation
)
and
![[eq43]](/images/importance-sampling__92.png)
The
function
attains its maximum at the point
and then rapidly goes to
for values of
that are smaller or larger than
.
On the contrary, the probability density function
of a standard normal random variable is almost zero at
.
As a consequence, if we use a standard Monte Carlo approximation, we extract
lots of values of
for which
is almost zero, but we extract very few values for which
is different from zero, and this results in a high variance of the
approximation error.
In order to shift weight towards
,
we can sample from
,
where
has a normal distribution with mean
and standard deviation
.
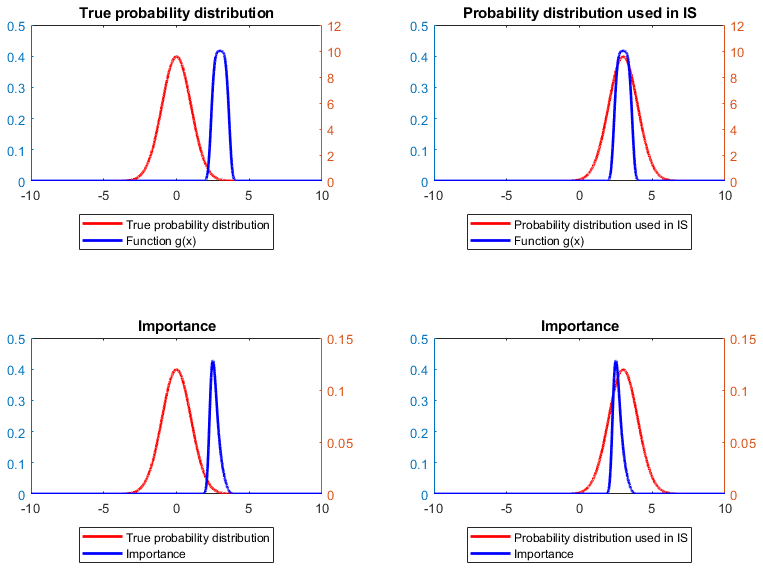
The following MATLAB code shows how to do so and computes the standard Monte
Carlo (MC) and the importance sampling
(IS) approximations by using samples of
independent draws from the distributions of
and
.
rng(0) n=10000; x=randn(n,1); g=10*exp(-5*(x-3).^4); MC=mean(g) stdMC=sqrt((1/n)*var(g)) y=3+randn(n,1); g=10*exp(-5*(y-3).^4); gWeighted=g.*normpdf(y,0,1)./normpdf(y,3,1); IS=mean(gWeighted) stdIS=sqrt((1/n)*var(gWeighted))
The standard deviations of the two approximations
(stdMC and stdIS) are
estimated by using the sample variances of
and
.
If you run the code you can see that indeed the importance sampling
approximation achieves a significant reduction in the approximation error
(from 0.0084 to 0.0012).
Most of the learning materials found on this website are now available in a traditional textbook format.
