Type I error

by Marco Taboga, PhD

In a test of hypothesis, a Type I error is committed when the null hypothesis is rejected despite being true.

Synonyms

Type I errors are also called errors of the first kind.

Explanation

When conducting a test of hypothesis, we decide whether to reject the null hypothesis or not to reject it.

Usually, the decision is taken based on the value of a test statistic:

• if the test statistic falls within a pre-specified critical region, then the null is rejected;

• otherwise, it is not rejected.

In doing so, we can incur in the following error: reject the null hypothesis when the null hypothesis is indeed true.

Errors of this kind are called Type I errors, as opposed to Type II errors, which occur when the null hypothesis is not rejected despite being wrong.

This can be summarized in the following diagram.

Probability of Type I errors

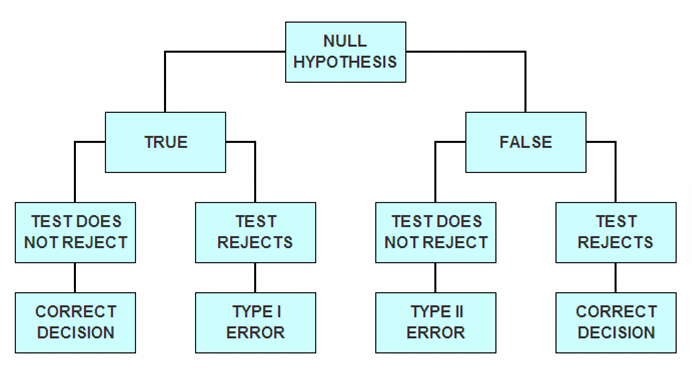
As we have already explained, in a test of hypothesis we look at the value taken by a test statistic, and based on this value we decide whether or not tho reject the null hypothesis.

The value of the test statistic depends on the data used to perform the test, which is random. Therefore, before observing the data, the test statistic can be seen as a random variable.

The probability of committing a Type I error is equal to the probability that the test statistic will fall within the critical region. It is calculated under the assumption that the null hypothesis is true.

This probability (or an upper bound to it) is called size of the test, or level of significance of the test.

Example

Suppose that we observe a sample of draws from a normal distribution.

The mean of the distribution is unknown and its variance is known.

Null hypothesis

We want to test the null hypothesis that the mean of the distribution is equal to zero:

Test statistic

As explained in the lecture on the size of a test, we can use the z-statistic as a test statistic.

First, we compute the sample mean

Then, we compute the z-statistic:where we set , according to our null hypothesis.

Critical value

We compare the value taken by the test statistic to a critical value .

In particular, we take a decision based on the following rule:

• if , then we do not reject the null hypothesis;

• if , then we reject the null hypothesis.

Incorrect decision

Suppose that the true mean is indeed equal to zero.

If , then the outcome of the test is a rejection of the null hypothesis .

This is a Type I error! We are rejecting the null when it is in fact true.

Probability of committing Type I errors

In this example, the probability of committing Type I errors is

Note that the probability needs to be calculated under the assumption that (i.e., under the assumption that the null hypothesis holds).

A formula for this probability is derived in the lecture entitled Hypothesis tests about the mean.

An example of how to apply the formula can be found in the lecture on the size of a test.

Trade-off

There is usually a trade-off between the probability of committing Type I errors and the probability of committing Type II errors: a test that is less likely to reject a correct hypothesis is usually also more likely not to reject an incorrect one.

More details

Type I errors are more thoroughly discussed in the lecture entitled Hypothesis testing.

Keep reading the glossary

Previous entry: Transformation theorem

Next entry: Type II error

How to cite

Please cite as:

Taboga, Marco (2021). "Type I error", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/Type-I-error.