A continuous random variable has two main characteristics:
the set of its possible values is uncountable;
we compute the probability that its value will belong to a given interval by integrating a function called probability density function.
On this page we provide a definition of continuous variable, we explain it in great detail, we provide several examples and we derive some interesting properties.
Table of contents
Here is a formal definition.
Definition
A random variable
is said to be continuous if and only if the probability that it will belong to
an interval
can be expressed as an
integral:
![[eq1]](/images/absolutely-continuous-random-variable__3.png) where
the integrand function
where
the integrand function
is called the probability density function of
.
If you are not familiar with integrals, you can read the lecture on the basics of integration.
It is anyway important to remember that an integral is used to compute an area under a curve.
In the definition of a continuous variable, the integral is the area under the
probability density function in the interval between
and
.
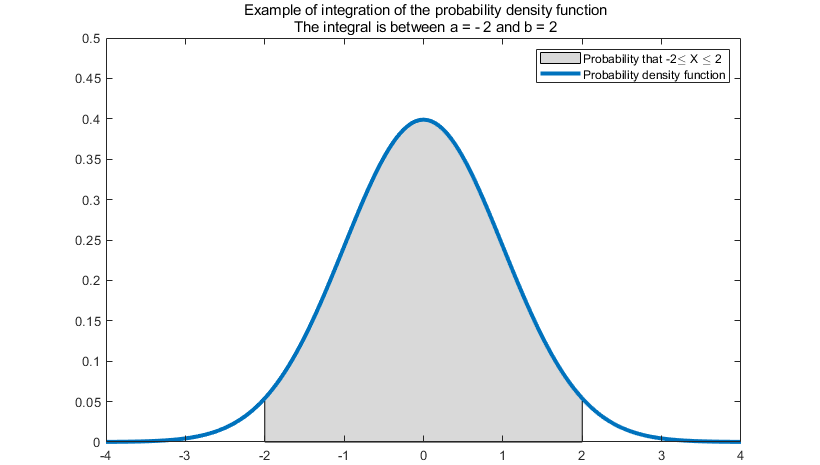
The first thing to note in the definition above is that the distribution of a continuous variable is characterized by assigning probabilities to intervals of numbers.
Contrast this with the fact that the distribution of a discrete variable is characterized by assigning probabilities to single numbers.
Before explaining why the distribution of a continuos variable is assigned by intervals, we make some examples and discuss some of its mathematical properties.
Here are some examples.
Let
be a continuous random variable that can take any value in the interval
.
Let its probability density function
be![[eq3]](/images/absolutely-continuous-random-variable__10.png)
Then, for example, the probability that
takes a value between
and
can be computed as
follows:
Let
be a continuous random variable that can take any value in the interval
with probability density
function
![[eq5]](/images/absolutely-continuous-random-variable__17.png)
The probability that the realization of
will belong to the interval
is
As a consequence of the definition above, the
cumulative distribution function of a
continuous variable
is
![]()
The derivative of an integral with respect to its upper bound of integration
is equal to the integrand function.
Therefore,
In other words, the probability density function
is the derivative of the cumulative distribution function
.
Any single realization
has zero probability of being observed
because
Therefore, in a continuous setting zero-probability events are not events that never happen. In fact, they do happen all the time: all the possible values have zero probability, but one of them must be the realized value.
This property, which may seem paradoxical, is discussed in the lecture on zero-probability events.
Another consequence of the definition given above is that the support of a continuous random variable must be uncountable.
In fact, by the previous property, if the support
(the set of values the variable can take) was countable, then we would
have
which
is a contradiction because the probability that a random variable takes at
least one of all its possible values must be 1.
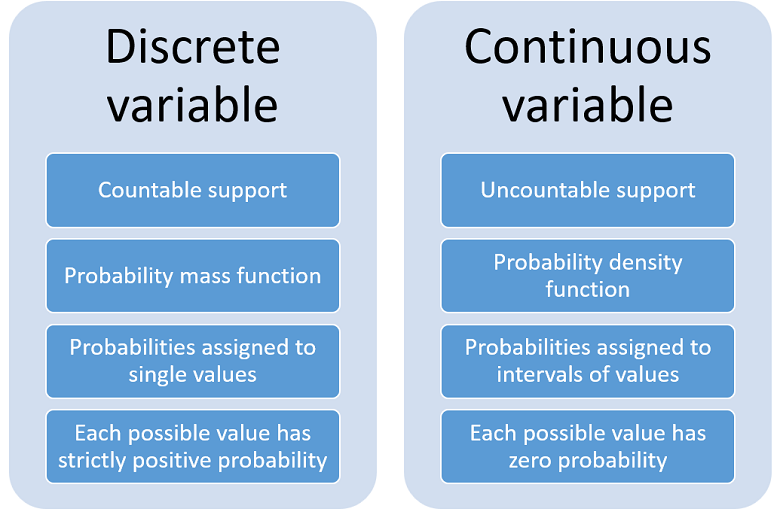
In order to sharpen our understanding of continuous variables, let us highlight the main differences with respect to discrete variables found so far.
The main characteristics of a discrete variable are:
the set of values it can take (so-called support) is countable;
its probability distribution is described by a probability mass function that assigns a probability to each single value in the support;
the values belonging to the support have a strictly positive probability of being observed.
By contrast, the main characteristics of a continuous random variable are:
the set of values it can take is uncountable;
its probability distribution is described by a probability density function that assigns probabilities to intervals of values;
each value belonging to the support has zero probability of being observed.
Why do we define a mathematical object that has such a counterintuitive property (all possible values have zero probability)?
The short answer is that we do it for mathematical convenience.
Suppose that we are trying to model a certain variable that we see as random, for example, the proportion of atoms that exhibit a certain behavior in a physics experiment.
In general, a proportion is a number in the interval
.
If we knew exactly the total number
of atoms involved in the experiment, then we would also know that the
proportion
could take the
values
However, in many cases the exact number of atoms involved in an experiment is not only huge, but also not known precisely.
What do we do in such cases? Can we enumerate all the possible values of
?
Theoretically, we could write down the list in (1) for every value of
that we deem possible and then take the union of all the lists.
The resulting union would be a finite support for our random variable
,
to which we would then need to assign probabilities.
Given that the possible values of
are likely in the trillions, such an approach would be highly impractical.
An alternative is to consider the set of all rational numbers belonging to the
interval
.
Remember that a rational number is the ratio of two integers. As a
consequence, the set of rational numbers in
includes all the possible values of the proportion
.
Moreover, it is a countable set.
Thus, we can use a probability mass function to assign probabilities to it, without resorting to exotic density functions.
Unfortunately, this approach works only in special cases.
For example, suppose that all the possible values of
are deemed to be equally likely. There is no way to assign equal probabilities
to all the values in the set of rational numbers in
because it contains infinitely many numbers (the probability of a single
number should be
,
which does not work).
The third alternative is provided by continuous random variables.
We can consider the whole interval of real numbers
and assign probabilities to its sub-intervals using a probability density
function.
In the case in which all the values are deemed equally likely, we use a
constant probability density function, equal to
on the whole interval (called a
uniform
distribution).
This brilliantly solves the problem, although we need to accept the fact that
the question "What is the probability that
will take a specific value
?"
does not make much sense any longer.
The questions that we can still ask are of the kind "What is the probability
that
will take a value close to
?"
provided that we define precisely what we mean by close in terms of an
interval (e.g.,
where
is an accuracy parameter that we define).
You can find other explanations and examples that help to understand the definition of continuous variable in:
this blog post on Math Insight;
these lecture notes used in the Mathematics Department of the University of Colorado Boulder;
our page on the probability density function.
The expected value of a continuous random variable is calculated
as
See the lecture on the expected value for explanations and examples.
The moments of a continuous variable can be computed
as![[eq16]](/images/absolutely-continuous-random-variable__53.png) and
the expected value of a transformation
and
the expected value of a transformation
is
![[eq17]](/images/absolutely-continuous-random-variable__55.png)
The variance can be computed by first calculating moments as above and then
using the variance
formula![]()
The conditional expected value of a continuous random variable can be calculated using its conditional density function (see the lecture on conditional expectation for details and examples).
The next table contains some examples of continuous distributions that are frequently encountered in probability theory and statistics.
| Name of the continuous distribution | Support |
|---|---|
| Uniform | All the real numbers in the interval [0,1] |
| Normal | The whole set of real numbers |
| Chi-square | The set of all non-negative real numbers |
Continuous random variables are sometimes also called absolutely continuous.
Continuous random variables are discussed also in:
the lecture on random variables;
the glossary entry on the probability density function.
Multivariate generalizations of the concept are presented here:
Next entry: Absolutely continuous random vector
Please cite as:
Taboga, Marco (2021). "Continuous random variable", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/absolutely-continuous-random-variable.
Most of the learning materials found on this website are now available in a traditional textbook format.