Random matrix

by Marco Taboga, PhD

A random matrix is a matrix whose entries are random variables.

Associated random vector

We can analyze a random matrix by studying the characteristics of its associated random vector, which is obtained by stacking the columns of the matrix.

For example, given a random matrixwe can study its associated vectorizationwhich is a random vector.

Another example is a random matrixwhose vectorization is

Thus, all the theory developed for random vectors applies to random matrices.

For example, a random matrix is said to be:

• discrete if the associated random vector is discrete;

• continuous if the associated random vector is continuous.

Random matrix theory

A flourishing area of modern mathematics, called random matrix theory, studies the distributional properties of some characteristics of random matrices such as their eigenvalues and determinants.

Important results in random matrix theory are:

1. the Wigner semicircle law (distribution of the eigenvalues of a symmetric matrix);

2. the Wigner surmise (distribution of the spaces between the eigenvalues);

3. the Circular law (distribution of the eigenvalues of a non-symmetric matrix);

4. the Tracy-Widom law (distribution of the largest eigenvalue of a matrix);

5. the Marchenko-Pastur law (distribution of the singular values of a matrix).

This blog post provides an elementary description of some of these results.

The most important matrix distribution

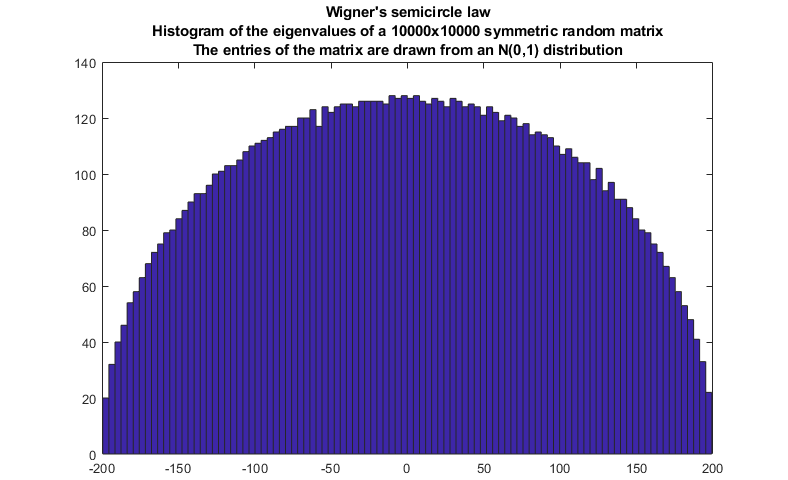
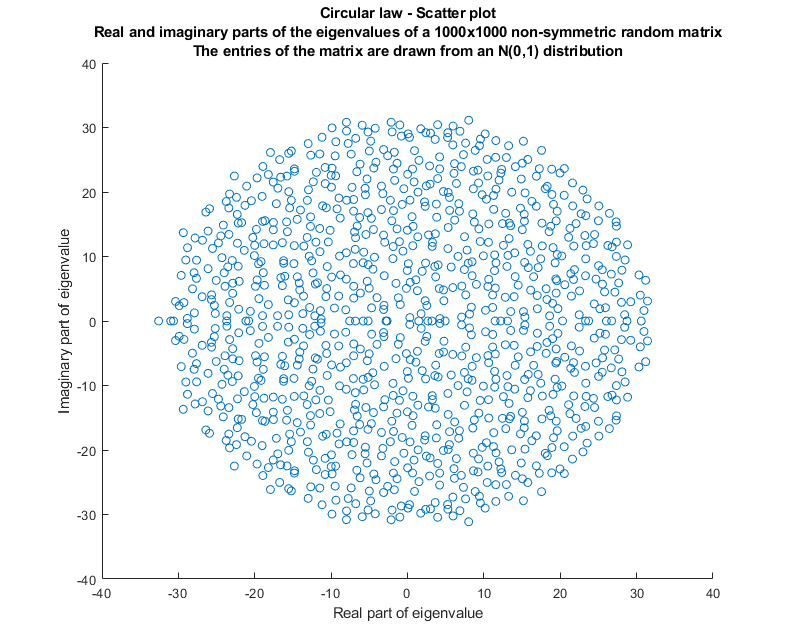
Probably, the most important random matrix distribution is the Wishart distribution. It is often used in probability and statistics and it has many interesting connections with other distributions such as the Gamma and the multivariate normal.

Other matrix distributions

Several other matrix distributions are used in mathematical and statistical applications.

Here is a list.

1. Generalizations of vector distributions:

   1. the Wishart distribution

   2. the Inverse Wishart distribution;

   3. the Matrix normal distribution;

   4. the Matrix Gamma distribution;

   5. the Inverse Matrix Gamma distribution;

   6. the Matrix t distribution;

   7. the Matrix F distribution;

   8. the Matrix beta distribution;

   9. the Matrix Dirichlet distribution;

   10. the Matrix Langevin distribution

   11. the Matrix Pareto distribution;

2. Gaussian distributions:

   1. the Gaussian Orthogonal matrix distribution;

   2. the Gaussian Unitary matrix distribution;

   3. the Gaussian Symplectic matrix distribution;

3. Circular distributions:

   1. the Circular Real matrix distribution;

   2. the Circular Unitary matrix distribution;

   3. the Circular Quaternion matrix distribution;

   4. the Circular Orthogonal matrix distribution;

   5. the Circular Symplectic matrix distribution.

Recent studies analyze also the properties of some discrete matrix distributions.

More details

Curious to know more about random matrix theory? Here are some suggestions:

• a primer by Julian Izenman;

• an introductory book by Giacomo Livan et al.;

• a more advanced book by Terence Tao.

Keep reading the glossary

Previous entry: Probability space

Next entry: Realization of a random variable

How to cite

Please cite as:

Taboga, Marco (2021). "Random matrix", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/random-matrix.