Index > Matrix algebra > Discrete Fourier Transform

Discrete Fourier transform of a real signal

This lecture discusses some important properties of the Discrete Fourier Transform of a real vector (signal).

Table of contents

The transform
Complex conjugation
Conjugate symmetry
First entry of the DFT
Nyquist frequency
Examples
1. Example 1 - N even
2. Example 2 - N odd
Representation in terms of sines and cosines
Amplitude spectrum
Power spectrum

The transform

In what follows, the Discrete Fourier Transform (DFT) of an vector is another vector whose entries satisfy [eq1] where is the imaginary unit.

Complex conjugation

We will repeatedly use some properties of complex conjugation, briefly reviewed here.

Remember that the complex conjugate of is

The complex conjugate of a sum is equal to the sum of the conjugates:

The complex conjugate of a product is equal to the product of the conjugates:

The complex conjugate of a complex exponential is

Conjugate symmetry

The DFT of a real signal enjoys the following conjugate symmetry property.

Proposition Let and be two vectors, such that is the Discrete Fourier Transform of . If all the entries of are real numbers, thenfor .

Proof

First of all, we apply the rules of complex conjugation: [eq8] In the last step, we have used the fact that the complex conjugate of a real number is equal to the number itself. Then, we exploit some basic properties of trigonometric functions: [eq9] Finally, we put together the previous results: [eq10]

First entry of the DFT

If the vector is real, then the first entry of its DFT () is also real.

Proof

It suffices to set in the DTF formula: [eq11] The result of the latter sum is real because all the summands are real by assumption.

Nyquist frequency

Consider the so-called Nyquist frequency .

If is an integer (i.e., is even) and the vector is real, then the DFT entry $X_{N/2+1}$ is also real.

Proof

By the conjugate symmetry property, we haveBut a complex number is equal to its conjugate only if it is real.

Examples

We now show a couple of numeric examples, where you can see that the properties above (conjugate symmetry, zero complex part for first and Nyquist entries) are satisfied.

Example 1 - N even

In the first example is even (equal to 8).

We mark symmetric terms with matching symbols.

Signal x	DFT X (real part)	DFT X (complex part)	Comments and symmetry marks
1.0000	10.0000	0	First entry (no complex part)
1.5000	-0.4464	-1.5364	*
1.7000	0.3000	0.1000	@
1.3000	-1.1536	0.2636	$
1.8000	0.6000	0	Nyquist folding (no complex part)
0.8000	-1.1536	-0.2636	$
0.8000	0.3000	-0.1000	@
1.1000	-0.4464	1.5364	*

Example 2 - N odd

In the second example is odd (equal to 9).

Signal x	DFT X (real part)	DFT X (complex part)	Comments and symmetry marks
0.5000	3.9000	0	First entry (no complex part)
-0.2000	-3.0670	-0.3692	*
-0.4000	1.7162	1.3334	@
1.1000	1.2000	-1.5588	$
1.8000	0.4508	0.1438	%
0.7000	0.4508	-0.1438	%
0.5000	1.2000	1.5588	$
0.2000	1.7162	-1.3334	@
-0.3000	-3.0670	0.3692	*

Representation in terms of sines and cosines

When is real, we can derive a frequency domain representation in terms of sines and cosines:

if is even, the representation is
if is odd, the representation iswhere denotes the floor of .

Proof

The usual frequency-domain representation is [eq16]

We will transform it, by using the following property, derived in the proofs above:

When is even, we have

[eq18] Therefore, [eq19] When is odd, an almost identical derivation yields [eq20]

Note that in both cases (even and odd), the representation involves only the first entries of the DFT.

The remaining entries of the DFT (those corresponding to frequencies higher than the Nyquist frequency) are not used in the representation.

In other words, when is real, the information about enclosed in the DFT is somehow redundant: the values of beyond the Nyquist frequency are not needed to reconstruct .

Amplitude spectrum

The amplitude spectrum is an vector whose entries are calculated as

As a direct consequence of the conjugate symmetry property derived previously, the amplitude spectrum of a real signal is symmetric around the Nyquist frequency:for .

Here is an example.

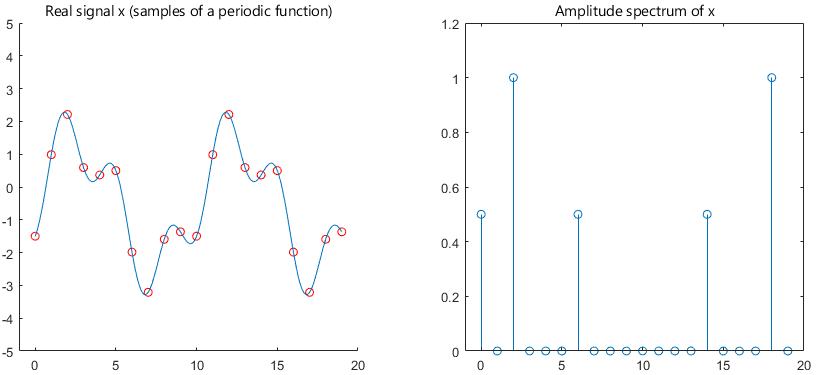
Plot of a real signal and its symmetric amplitude spectrum.

Power spectrum

The entries of the power spectrum satisfy

Therefore, also the power spectrum is symmetric.

How to cite

Please cite as:

Taboga, Marco (2021). "Discrete Fourier transform of a real signal", Lectures on matrix algebra. https://www.statlect.com/matrix-algebra/discrete-Fourier-transform-of-a-real-signal.