Search for probability and statistics terms on Statlect
StatLect
Index > Matrix algebra

Linear independence of eigenvectors

by , PhD

Eigenvectors corresponding to distinct eigenvalues are linearly independent. As a consequence, if all the eigenvalues of a matrix are distinct, then their corresponding eigenvectors span the space of column vectors to which the columns of the matrix belong.

If there are repeated eigenvalues, but they are not defective (i.e., their algebraic multiplicity equals their geometric multiplicity), the same spanning result holds.

However, if there is at least one defective repeated eigenvalue, then the spanning fails.

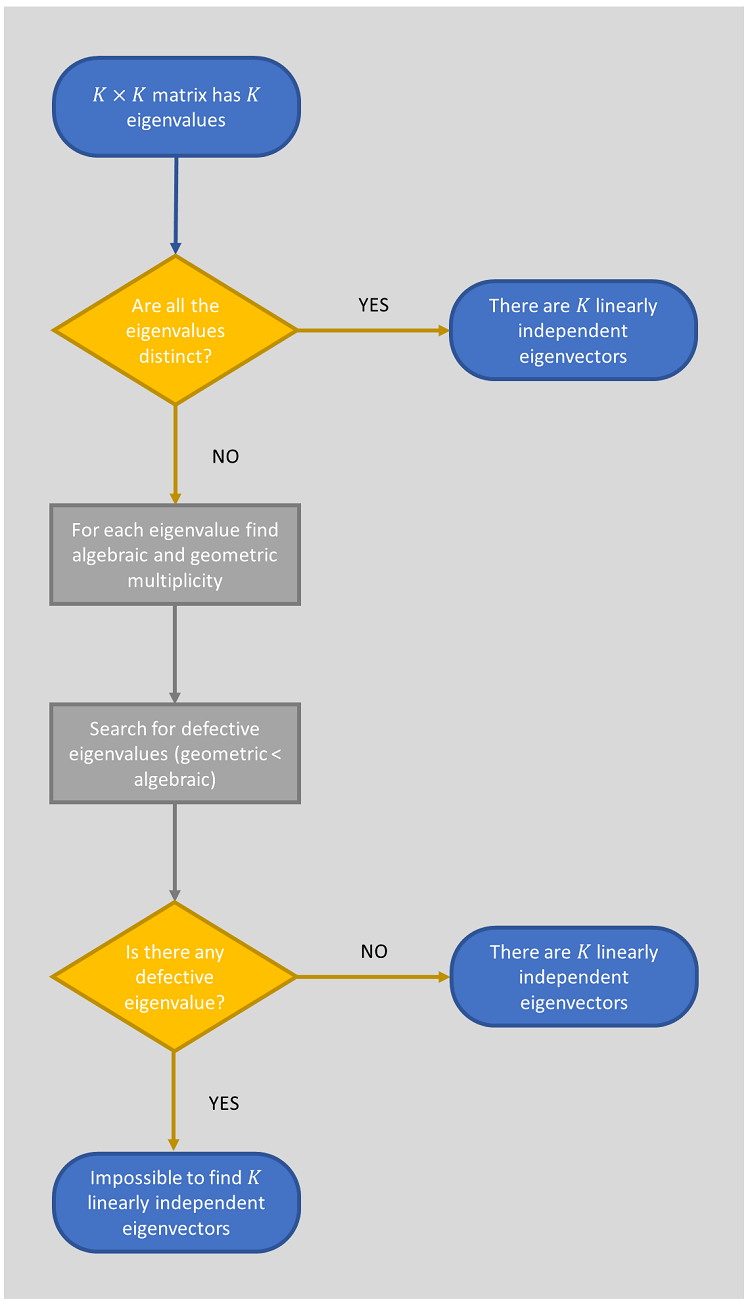
Flowchart explaining how to decide whether there is a basis of eigenvectors by checking geometric and algebraic multiplicities.

These results will be formally stated, proved and illustrated in detail in the remainder of this lecture.

Table of Contents

Independence of eigenvectors corresponding to different eigenvalues

We now deal with distinct eigenvalues.

Proposition Let A be a $K imes K$ matrix. Let [eq1] ($Mleq $ K) be eigenvalues of A and choose [eq2] associated eigenvectors. If there are no repeated eigenvalues (i.e., [eq3] are distinct), then the eigenvectors [eq4] are linearly independent.

Proof

The proof is by contradiction. Suppose that [eq4] are not linearly independent. Denote by I the largest number of linearly independent eigenvectors. If necessary, re-number eigenvalues and eigenvectors, so that [eq6] are linearly independent. Note that $Igeq 1$ because a single vector trivially forms by itself a set of linearly independent vectors. Moreover, $I<M$ because otherwise [eq7] would be linearly independent, a contradiction. Now, $x_{I+1}$ can be written as a linear combination of [eq8]:[eq9]where [eq10] are scalars and they are not all zero (otherwise $x_{I+1}$ would be zero and hence not an eigenvector). By the definition of eigenvalues and eigenvectors we have that[eq11]and that[eq12]
By subtracting the second equation from the first, we obtain[eq13]Since [eq14] are distinct, [eq15] for $i=1,ldots ,I$. Furthermore, [eq16] are linearly independent, so that their only linear combination giving the zero vector has all zero coefficients. As a consequence, it must be that [eq17]. But we have already explained that these coefficients cannot all be zero. Thus, we have arrived at a contradiction, starting from the initial hypothesis that [eq4] are not linearly independent. Therefore, [eq4] must be linearly independent.

When $M=K$ in the proposition above, then there are K distinct eigenvalues and K linearly independent eigenvectors, which span (i.e., they form a basis for) the space of K-dimensional column vectors (to which the columns of A belong).

Example Define the $3 imes 3$ matrix[eq20]It has three eigenvalues[eq21]with associated eigenvectors[eq22]which you can verify by checking that [eq23] (for $k=1,ldots ,3$). The three eigenvalues $lambda _{1}$, $lambda _{2}$ and $lambda _{3}$ are distinct (no two of them are equal to each other). Therefore, the three corresponding eigenvectors $x_{1}$, $x_{2}$ and $x_{3}$ are linearly independent, which you can also verify by checking that none of them can be written as a linear combination of the other two. These three eigenvectors form a basis for the space of all $3 imes 1$ vectors, that is, a vector[eq24]can be written as a linear combination of the eigenvectors $x_{1}$, $x_{2}$ and $x_{3}$ for any choice of the entries $alpha $, $beta $ and $gamma $.

Independence of eigenvectors when no repeated eigenvalue is defective

We now deal with the case in which some of the eigenvalues are repeated.

Proposition Let A be a $K imes K$ matrix. If A has some repeated eigenvalues, but they are not defective (i.e., their geometric multiplicity equals their algebraic multiplicity), then there exists a set of K linearly independent eigenvectors of A.

Proof

Denote by [eq25] the K eigenvalues of A and by [eq26] a list of corresponding eigenvectors chosen in such a way that $x_{j}$ is linearly independent of $x_{k}$ whenever there is a repeated eigenvalue [eq27]. The choice of eigenvectors can be performed in this manner because the repeated eigenvalues are not defective by assumption. Now, by contradiction, suppose that [eq28] are not linearly independent. Then, there exist scalars [eq29] not all equal to zero such that[eq30]Denote by $M$ the number of distinct eigenvalues. Without loss of generality (i.e., after re-numbering the eigenvalues if necessary), we can assume that the first $M$ eigenvalues are distinct. For $m=1,ldots ,M$, define the sets of indices corresponding to groups of equal eigenvalues[eq31]and the vectors[eq32]Then, equation (1) becomes[eq33]Denote by $J$ the following set of indices:[eq34]The set $J$ must be non-empty because [eq35] are not all equal to zero and the previous choice of linearly independent eigenvectors corresponding to a repeated eigenvalue implies that the vectors $u_{m}$ in equation (2) cannot be made equal to zero by appropriately choosing positive coefficients $c_{k}$. Then, we have[eq36]But, for any $jin J$, $u_{j}$ is an eigenvector (because eigenspaces are closed with respect to linear combinations). This means that a linear combination (with coefficients all equal to 1) of eigenvectors corresponding to distinct eigenvalues is equal to 0. Hence, those eigenvectors are linearly dependent. But this contradicts the fact, proved previously, that eigenvectors corresponding to different eigenvalues are linearly independent. Thus, we have arrived at a contradiction. Hence, the initial claim that [eq37] are not linearly independent must be wrong. As a consequence, [eq38] are linearly independent.

Thus, when there are repeated eigenvalues, but none of them is defective, we can choose K linearly independent eigenvectors, which span the space of K-dimensional column vectors (to which the columns of A belong).

Example Define the $3 imes 3$ matrix[eq39]It has three eigenvalues[eq40]with associated eigenvectors[eq41]which you can verify by checking that [eq23] (for $k=1,ldots ,3$). The three eigenvalues are not distinct because there is a repeated eigenvalue [eq43] whose algebraic multiplicity equals two. However, the two eigenvectors $x_{1}$ and $x_{2}$ associated to the repeated eigenvalue are linearly independent because they are not a multiple of each other. As a consequence, also the geometric multiplicity equals two. Thus, the repeated eigenvalue is not defective. Therefore, the three eigenvectors $x_{1}$, $x_{2}$ and $x_{3}$ are linearly independent, which you can also verify by checking that none of them can be written as a linear combination of the other two. These three eigenvectors form a basis for the space of all $3 imes 1$ vectors.

Defective matrices do not have a complete basis of eigenvectors

The last proposition concerns defective matrices, that is, matrices that have at least one defective eigenvalue.

Proposition Let A be a $K imes K$ matrix. If A has at least one defective eigenvalue (whose geometric multiplicity is strictly less than its algebraic multiplicity), then there does not exist a set of K linearly independent eigenvectors of A.

Proof

Remember that the geometric multiplicity of an eigenvalue cannot exceed its algebraic multiplicity. As a consequence, even if we choose the maximum number of independent eigenvectors associated to each eigenvalue, we can find at most $K-1$ of them because there is at least one defective eigenvalue.

Thus, in the unlucky case in which A is a defective matrix, there is no way to form a basis of eigenvectors of A for the space of K-dimensional column vectors to which the columns of A belong.

Example Consider the $2 imes 2$ matrix[eq44]The characteristic polynomial is[eq45]and its roots are[eq46]Thus, there is a repeated eigenvalue ([eq47]) with algebraic multiplicity equal to 2. Its associated eigenvectors [eq48]solve the equation[eq49]or[eq50]which is satisfied for $x_{11}=0$ and any value of $x_{21}$. Hence, the eigenspace of $lambda _{1}$ is the linear space that contains all vectors $x_{1}$ of the form[eq51]where $alpha $ can be any scalar. In other words, the eigenspace of $lambda _{1}$ is generated by a single vector[eq52]Hence, it has dimension 1 and the geometric multiplicity of $lambda _{1}$ is 1, less than its algebraic multiplicity, which is equal to 2. This implies that there is no way of forming a basis of eigenvectors of A for the space of two-dimensional column vectors. For example, the vector[eq53]cannot be written as a multiple of the eigenvector $x_{1}$. Thus, there is at least one two-dimensional vector that cannot be written as a linear combination of the eigenvectors of A.

Solved exercises

Below you can find some exercises with explained solutions.

Exercise 1

Consider the matrix $2 imes 1$[eq54]

Try to find a set of eigenvectors of A that spans the set of all $2 imes 1 $ vectors.

Solution

The characteristic polynomial is[eq55]and its roots are[eq56]Since there are two distinct eigenvalues, we already know that we will be able to find two linearly independent eigenvectors. Let's find them. The eigenvector [eq48]associated to $lambda _{1}$ solves the equation[eq58]or[eq59]which is satisfied for any couple of values $x_{11},x_{21}$ such that [eq60]or [eq61]For example, we can choose $x_{21}=2$, so that $x_{11}=-3$ and the eigenvector associated to $lambda _{1}$ is[eq62]The eigenvector [eq63]associated to $lambda _{2}$ solves the equation[eq64]or[eq65]which is satisfied for any couple of values $x_{12},x_{22}$ such that [eq66]or [eq67]For example, we can choose $x_{12}=1$, so that $x_{22}=1$ and the eigenvector associated to $lambda _{2}$ is[eq68]Thus, $x_{1}$ and $x_{2}$ form the basis of eigenvectors we were searching for.

Exercise 2

Define[eq69]

Try to find a set of eigenvectors of A that spans the set of all column vectors having the same dimension as the columns of A.

Solution

The characteristic polynomial is[eq70]where in step $frame{A}$ we have used the Laplace expansion along the third row. The roots of the polynomial are[eq71]Hence, [eq72] is a repeated eigenvalue with algebraic multiplicity equal to 2. Its associated eigenvectors [eq73]solve the equation[eq74]or[eq75]This system of equations is satisfied for any value of $x_{22}$ and $x_{12}=x_{32}=0$. As a consequence, the eigenspace of $lambda _{2}$ contains all the vectors $x_{2}$ that can be written as[eq76]where the scalar $x_{22}$ can be arbitrarily chosen. Thus, the eigenspace of $lambda _{2}$ is generated by a single vector[eq77]Hence, the eigenspace has dimension 1 and the geometric multiplicity of $lambda _{2}$ is 1, less than its algebraic multiplicity, which is equal to 2. It follows that the matrix A is defective and we cannot construct a basis of eigenvectors of A that spans the space of $3 imes 1$ vectors.

How to cite

Please cite as:

Taboga, Marco (2021). "Linear independence of eigenvectors", Lectures on matrix algebra. https://www.statlect.com/matrix-algebra/linear-independence-of-eigenvectors.

The books

Most of the learning materials found on this website are now available in a traditional textbook format.

Featured pages
Explore
Main sections
About
Glossary entries
Share
  • To enhance your privacy,
  • we removed the social buttons,
  • but don't forget to share.