Sample variance

by Marco Taboga, PhD

Given a number of observations, their sample variance measures how far they are spread apart. It is also an estimator of the variance of the population from which the observations have been drawn.

Formulae

Given observations having sample mean there are two main ways to compute the sample variance:

• unadjusted sample variance, also called biased sample variance:

• adjusted sample variance, also called unbiased sample variance:

Example

Suppose we observe four realizations:

Their sample mean is:

Dividing the sum of squared deviations from the mean by the number of observations, we obtain the unadjusted sample variance:

Dividing it by the number of observations minus one, we instead obtain the unbiased estimate:

How to calculate the sample variance using a table

When there are many observations, it may be convenient to organize the calculations into a table.

In the previous example, the calculations could have been performed as follows.

Observation number	Value	Deviation from mean	Squared deviation
1	4	-1	1
2	4	-1	1
3	5	0	0
4	7	2	4
Sum	20	0	6
Divide sum by n	5		3/2
Divide sum by n-1			2

The sample variances are on the last two rows of the table.

Dispersion

The sample variance is a measure of dispersion of the observations around their sample mean.

A squared deviation quantifies how far an observation is from the mean.

The sample variance, being an average of the squared deviations, measures the average distance (or spread) from the mean.

Sample variance and population variance

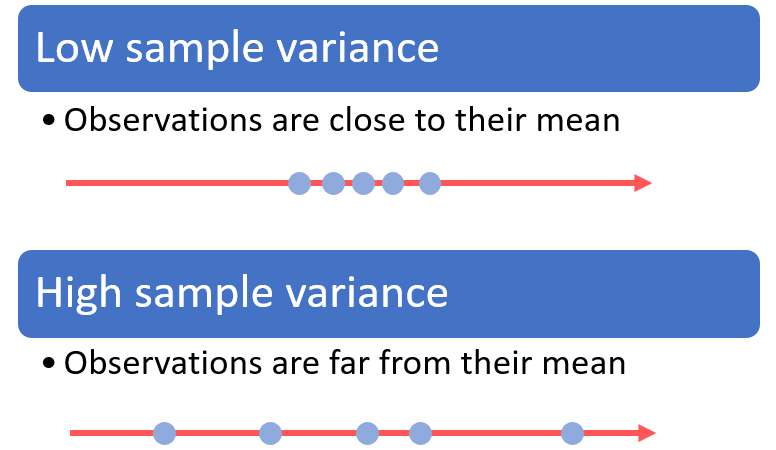
Assume that the observations are all drawn from the same probability distribution.

Then, the variance of that probability distribution is called population variance.

When the observations are independent, is a biased estimator of the population variance, while is unbiased.

More details

The lecture entitled Variance estimation provides more details about the sample variance, including derivations of its properties, examples and exercises.

Keep reading the glossary

Previous entry: Sample space

Next entry: Score vector

How to cite

Please cite as:

Taboga, Marco (2021). "Sample variance", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/sample-variance.