In a probabilistic experiment, the sample space is the set of all possible outcomes of the experiment.
The sample space is often denoted by the Greek letter
(Omega).
A possible outcome, which can also be called a
sample point, is indicated as
,
where
(omega) is the lowercase version of
.
The letter
is the last letter of the Greek alphabet and it is often linked to the idea of
something omnicomprehensive (in our case the set of all things that can
possibly happen). See also the related
Wikipedia article.
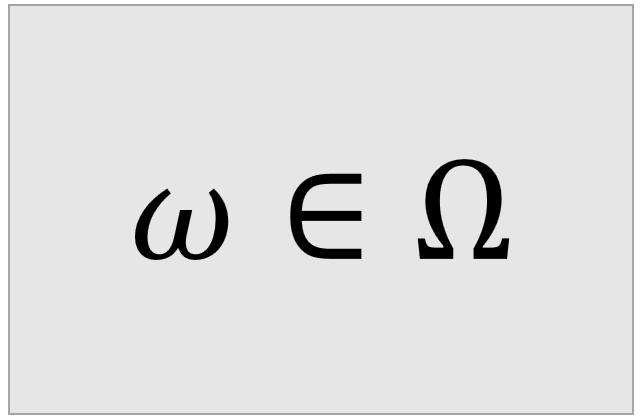
Here are some simple examples.
Example
Suppose that the probabilistic experiment is the
toss of a die. The six
numbers that can appear face up, from 1 to 6, are the six possible outcomes of
the experiment. Hence, the sample space
is![[eq1]](/images/sample-space__6.png){kind=small}
Example
When the experiment is the
flip of a coin,
there are two sample points, heads
and tails
.
The sample space
is![[eq2]](/images/sample-space__9.png){kind=small}
Example
When we flip two coins, there are four possible outcomes and the sample space
is![[eq3]](/images/sample-space__10.png){kind=small}
The sample space in the last example is a product space. It is obtained by combining the sample spaces of two experiments (two individual flips of a coin).
In general, if we repeat a probabilistic experiment two times, then the product space is the Cartesian product of the sample spaces of the two experiments.
The Cartesian product is the set of all possible couples of sample points, where the first point is taken from the sample space of the first experiment and the second point is taken from the sample space of the second experiment.
Example
In a first experiment, we randomly pick one of the first two letters of the
alphabet. The sample space
is![[eq4]](/images/sample-space__11.png){kind=small}
In
a second experiment, the sample space
is![[eq5]](/images/sample-space__12.png){kind=small}
Then,
the product space
is![[eq6]](/images/sample-space__13.png){kind=small}
If there are more than two experiments, we follow the same logic. For three experiments, we list all possible triplets; for four, we list the quadruplets, and so on.
In probability theory and statistics, it is quite common to deal with infinite sample spaces, made up of an infinite number of sample points.
This happens, for example, when a probabilistic experiment is repeated indefinitely until a certain condition is met.
Example
We flip a coin until we get heads. It is quite likely that we will obtain
heads after few throws. However, there is no upper bound on the number of
tosses required to meet the stopping criterion. For example, it is very likely
that we will get heads at least once in the first one hundred tosses, but
there is also a very small chance of observing one hundred tails in a row.
Similarly for one thousand, one million, and so on. Therefore, if we want to
properly enumerate all the possible outcomes, we need to consider an infinite
sample space, equal to the product of infinite individual
experiments:![[eq7]](/images/sample-space__14.png){kind=small}
As you probably know, infinite sets come in different sizes:
countably infinite sets, whose elements can be put in one-to-one correspondence with the set of natural numbers;
uncountably infinite sets, for which such a correspondence cannot be found.
Sample spaces can be not only countably infinite, as in the previous example, but also uncountable. Actually, both types are very common in statistics.
If you are not familiar with these two kinds of infinity, we suggest that you read two marvellous Scientific American articles on the topic:
A longer discussion can be found in a chapter of the Handbook of the Philosophy of Science by Peter Fletcher.
Frequently used uncountable sample spaces are the set of real numbers
and its sub-intervals, such as the interval
![$\left[ 0,1\right] $](/images/sample-space__16.png){kind=small}
.
How do these infinite spaces arise? How could they possibly describe a real-world probabilistic experiment?
Although admittedly unrealistic, they are typically used because of their mathematical convenience.
Example
Consider a physics experiment in which the proportion of atoms exhibiting a
certain behavior is seen as random. A proportion is a number in the interval
.
If we knew exactly the total number of atoms involved in the experiment
(easily a huge number!), we could enumerate all the possible values of the
proportion, and we would have a finite sample space. However, it is much more
convenient to assume that the sample space is the whole interval
.
For more details about this example, read our lecture on
continuous random
variables.
A detailed mathematical presentation of the concept of sample space - including a discussion of the properties that a sample space needs to satisfy - can be found in the lecture on Probability.
Previous entry: Sample size
Next entry: Sample variance
Please cite as:
Taboga, Marco (2021). "Sample space", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/sample-space.
Most of the learning materials found on this website are now available in a traditional textbook format.
