Search for probability and statistics terms on Statlect
StatLect
Index > Fundamentals of probability

Linear correlation

by , PhD

Linear correlation is a measure of dependence between two random variables.

It has the following characteristics:

Scatter plots of couples of random variables having different correlation coefficients.

Table of Contents

Definition

Let X and Y be two random variables.

The linear correlation coefficient (or Pearson's correlation coefficient) between X and Y is [eq1]where:

The linear correlation coefficient is well-defined only as long as [eq5], [eq6] and [eq7] exist and are well-defined.

It is often denoted by $ ho _{XY}$.

Zero standard deviations

In principle, the ratio is well-defined only if [eq8] and [eq4] are strictly greater than zero.

However, it is often assumed that [eq10] when one of the two standard deviations is zero.

This is equivalent to assuming that [eq11] because [eq12] when one of the two standard deviations is zero.

Interpretation

The interpretation is similar to the interpretation of covariance: the correlation between X and Y provides a measure of how similar their deviations from the respective means are (see the lecture on Covariance for a detailed explanation).

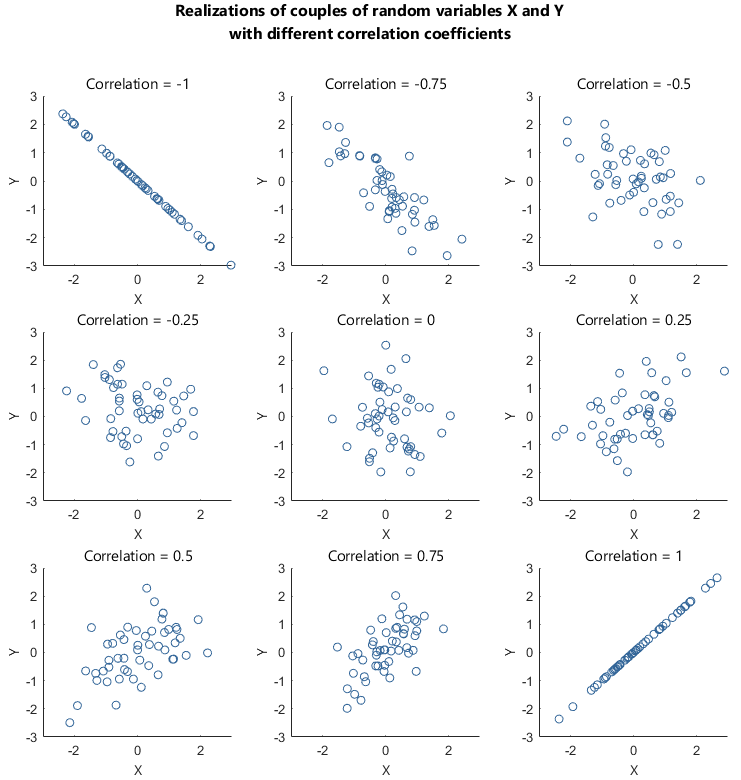
Linear correlation ranges between $-1$ and 1:[eq13]

Thanks to this property, correlation allows us to easily understand the intensity of the linear dependence between two random variables:

Terminology

The following terminology is often used:

  1. If [eq14] then X and Y are said to be positively linearly correlated (or simply positively correlated).

  2. If [eq15] then X and Y are said to be negatively linearly correlated (or simply negatively correlated).

  3. If [eq16] then X and Y are said to be linearly correlated (or simply correlated).

  4. If [eq10] then X and Y are said to be uncorrelated. Also note that [eq18] $=0$. Therefore, two random variables X and Y are uncorrelated whenever [eq19].

Example

In this example we show how to compute the coefficient of linear correlation between two discrete random variables.

Let X be a $2$-dimensional random vector and denote its entries by X_1 and X_2.

Let the support of X be [eq20]and its joint probability mass function be[eq21]

The support of X_1 is[eq22]and its probability mass function is[eq23]

The expected value of X_1 is[eq24]

The expected value of $X_{1}^{2}$ is[eq25]

The variance of X_1 is[eq26]

The standard deviation of X_1 is[eq27]

The support of X_2 is:[eq28]and its probability mass function is[eq29]

The expected value of X_2 is[eq30]

The expected value of $X_{2}^{2}$ is[eq31]

The variance of X_2 is[eq32]

The standard deviation of X_2 is[eq33]

Using the transformation theorem, we can compute the expected value of $X_{1}X_{2}$:[eq34]

Hence, the covariance between X_1 and X_2 is[eq35]and the linear correlation coefficient is[eq36]

More details

The following sections contain more details about the linear correlation coefficient.

Correlation of a random variable with itself

Let X be a random variable, then[eq37]

Proof

This is proved as follows:[eq38]where we have used the fact that[eq39]

Symmetry

The linear correlation coefficient is symmetric:[eq40]

Proof

This is proved as follows:[eq41]where we have used the fact that covariance is symmetric:[eq42]

Solved exercises

Below you can find some exercises with explained solutions.

Exercise 1

Let X be a $2 imes 1$ discrete random vector and denote its components by X_1 and X_2.

Let the support of X be[eq43]and its joint probability mass function be[eq44]

Compute the coefficient of linear correlation between X_1 and X_2.

Solution

The support of X_1 is[eq45]and its marginal probability mass function is[eq46]The expected value of X_1 is[eq47]The expected value of $X_{1}^{2}$ is[eq48]The variance of X_1 is[eq49]The standard deviation of X_1 is[eq50]The support of X_2 is[eq51]and its marginal probability mass function is[eq52]The expected value of X_2 is[eq53]The expected value of $X_{2}^{2}$ is[eq54]The variance of X_2 is[eq55]The standard deviation of X_1 is[eq56]Using the transformation theorem, we can compute the expected value of $X_{1}X_{2}$:[eq57]Hence, the covariance between X_1 and X_2 is[eq58]and the coefficient of linear correlation between X_1 and X_2 is[eq59]

Exercise 2

Let X be a $2 imes 1$ discrete random vector and denote its entries by X_1 and X_2.

Let the support of X be[eq60]and its joint probability mass function be[eq61]

Compute the coefficient of linear correlation between X_1 and X_2.

Solution

The support of X_1 is[eq62]and its marginal probability mass function is[eq63]The mean of X_1 is[eq64]The expected value of $X_{1}^{2}$ is[eq65]The variance of X_1 is[eq66]The standard deviation of X_1 is[eq67]The support of X_2 is[eq68]and its probability mass function is[eq69]The mean of X_2 is[eq70]The expected value of $X_{2}^{2}$ is[eq71]The variance of X_2 is[eq72]The standard deviation of X_2 is[eq73]The expected value of the product $X_{1}X_{2}$ can be derived using the transformation theorem[eq74]Therefore, putting pieces together, the covariance between X_1 and $X_{2} $ is[eq75]and the coefficient of linear correlation between X_1 and X_2 is[eq76]

Exercise 3

Let [eq77] be a continuous random vector with support [eq78]and let its joint probability density function be[eq79]

Compute the coefficient of linear correlation between X and Y.

Solution

The support of Y is[eq80]When $y otin R_{Y}$, the marginal probability density function of Y is 0, while, when $yin R_{Y}$, the marginal probability density function of Y can be obtained by integrating x out of the joint probability density as follows:[eq81]Thus, the marginal probability density function of Y is[eq82]The expected value of Y is[eq83]The expected value of $Y^{2}$ is[eq84]The variance of Y is[eq85]The standard deviation of Y is[eq86]The support of X is[eq87]When $x otin R_{X}$, the marginal probability density function of X is 0, while, when $xin R_{X}$, the marginal probability density function of X can be obtained by integrating $y$ out of the joint probability density as follows:[eq88]We do not explicitly compute the integral, but we write the marginal probability density function of X as follows:[eq89]The expected value of X is[eq90]The expected value of $X^{2}$ is[eq91]The variance of X is[eq92]The standard deviation of X is[eq93]The expected value of the product $XY$ can be computed by using the transformation theorem:[eq94]Hence, by the covariance formula, the covariance between X and Y is[eq95]and the coefficient of linear correlation between X and Y is[eq96]

How to cite

Please cite as:

Taboga, Marco (2021). "Linear correlation", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-probability/linear-correlation.

The books

Most of the learning materials found on this website are now available in a traditional textbook format.

Featured pages
Explore
Main sections
About
Glossary entries
Share
  • To enhance your privacy,
  • we removed the social buttons,
  • but don't forget to share.