A transformation theorem is one of several related results about the moments and the probability distribution of a transformation of a random variable (or vector).
Table of contents
Suppose that
![]() is a random
variable whose distribution is known.
is a random
variable whose distribution is known.
Given a function
![]() ,
how do we derive the distribution of
,
how do we derive the distribution of
![]() ?
?
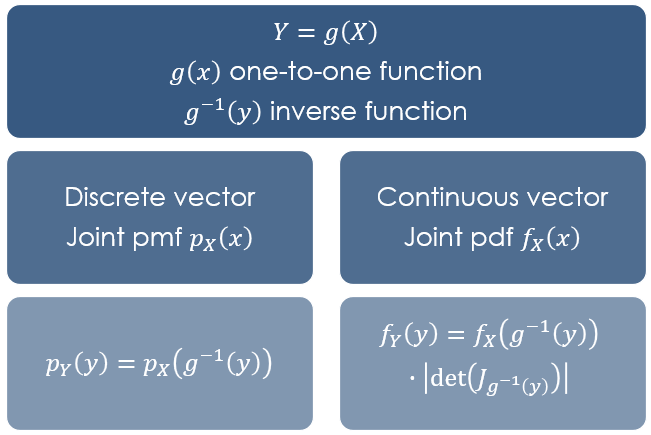
If the function
![]() is one-to-one (e.g., strictly increasing or strictly decreasing), there are
formulae for the probability mass (or density) and the
distribution function of
is one-to-one (e.g., strictly increasing or strictly decreasing), there are
formulae for the probability mass (or density) and the
distribution function of
![]() .
.
These formulae, sometimes called transformation theorems, are explained and proved in the lecture on functions of random variables.
Their generalization to the multivariate case (when
![]() is a random vector) are discussed in the lecture on
functions
of random vectors.
is a random vector) are discussed in the lecture on
functions
of random vectors.
When the function
![]() is not one-to-one and there are no simple ways to derive the distribution of
is not one-to-one and there are no simple ways to derive the distribution of
![]() ,
we can nonetheless easily compute the expected value and other moments of
,
we can nonetheless easily compute the expected value and other moments of
![]() ,
thanks to the so-called
Law
Of the Unconscious Statistician (LOTUS).
,
thanks to the so-called
Law
Of the Unconscious Statistician (LOTUS).
The LOTUS, illustrated below, is also often called transformation theorem.
For discrete random variables, the theorem is as follows.
Proposition
Let
![]() be a discrete random variable and
be a discrete random variable and
![]() a function.
Define
a function.
Define![]() Then,
Then,![[eq4]](/images/transformation-theorem__13.png) where
where
![]() is the support of
is the support of
![]() and
and
![]() is its probability mass function.
is its probability mass function.
Note that the above formula does not require us to know the support and the
probability mass function of
![]() ,
unlike the standard
formula
,
unlike the standard
formula![[eq6]](/images/transformation-theorem__18.png)
For continuous random variables, the theorem is as follows.
Proposition
Let
![]() be a continuous random variable and
be a continuous random variable and
![]() a function.
Define
a function.
Define![]() Then,
Then,![[eq9]](/images/transformation-theorem__22.png) where
where
![]() is the probability density
function of
is the probability density
function of
![]() .
.
Again, the above formula does not require us to know the probability density
function of
![]() ,
unlike the standard
formula
,
unlike the standard
formula![]()
The LOTUS can be used to compute any
moment of
![]() ,
provided that the moment
exists:
,
provided that the moment
exists:![[eq12]](/images/transformation-theorem__28.png)
The LOTUS can be used to compute the
moment
generating function (mgf)
![]()
The mgf completely characterizes the distribution of
![]() .
.
If we are able to calculate the above expected value and we recognize that
![]() is the joint mgf of a known distribution, then that distribution is the
distribution of
is the joint mgf of a known distribution, then that distribution is the
distribution of
![]() .
In fact, two random variables have the same distribution if and only if they
have the same mgf, provided the latter exists.
.
In fact, two random variables have the same distribution if and only if they
have the same mgf, provided the latter exists.
Similar comments apply to the
characteristic
function![]()
More details about the transformation theorem can be found in the following lectures:
Abadir, K.M. and Magnus, J.R., 2007. A statistical proof of the transformation theorem. The Refinement of Econometric Estimation and Test Procedures, Cambridge University Press.
Goldstein, J.A., 2004. An appreciation of my teacher, MM Rao. In Stochastic Processes and Functional Analysis (pp. 31-34). CRC Press.
Schervish, M.J., 2012. Theory of statistics. Springer Science & Business Media.
Previous entry: Test statistic
Next entry: Type I error
Please cite as:
Taboga, Marco (2021). "Transformation theorem", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/transformation-theorem.
Most of the learning materials found on this website are now available in a traditional textbook format.