Covariance stationary

by Marco Taboga, PhD

A sequence of random variables is covariance stationary if:

• all the terms of the sequence have the same mean;

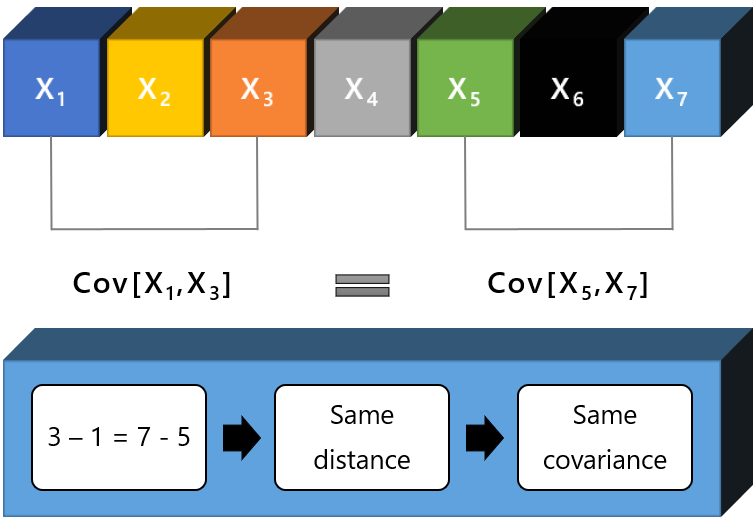
• the covariance between any two terms of the sequence depends only on the relative position of the two terms and not on their absolute position.

By relative position of two terms we mean how far apart they are located from each other in the sequence.

Instead, the absolute position refers to where they are located in the sequence.

Synonyms

Covariance stationary sequences are also called:

• weakly stationary sequences;

• covariance stationary processes;

• weakly stationary processes.

Often, we also use the term time series instead of sequence or process.

Definition

This is a formal definition.

In words:

1. all the terms of the sequence have mean ;

2. the covariance depends only on the relative position and not on the absolute position .

Note thatwhich implies that a weakly stationary process has constant variance.

Definition for random vectors

The definition above applies without modifications to sequences of random vectors.

In the case of a sequence of vectors, is a vector of expected values and is a matrix of covariances between the entries of the two vectors and (a cross-covariance matrix).

Examples

Let us make some examples.

Example 1 - White noise

The simplest example is the so called white noise process, a sequence that satisfies the following three conditions for any and :where is a positive constant.

Example 2 - Autoregressive process

Let be the white noise process of the previous example.

A first-order autoregressive process is a sequence whose terms satisfywhere is a constant and the recursion starts from a random variable uncorrelated with the terms of .

The expected values of the terms of the sequence are

For the process to be weakly stationary, the first condition that needs to be satisfied is which is satisfied only if or . The latter possibility wil be ruled out below.

The variances are

The variances remain finite as grows only if . Furthermore, the conditionis satisfied only ifwhich can be shown, for example, by solving

As proved in the lecture on autocorrelation, the covariance between any two terms of the sequence iswhich satisfies the condition stated in the definition of weak stationarity (the covariance depends only on ).

Thus, the sequence is covariance stationary only if

Weakly vs strictly stationary

A stronger concept of stationarity is that of strict stationarity.

A sequence is said to be strictly stationary if and only if and have the same joint distribution for any , and .

How covariance stationarity is used

The concept of covariance stationarity is often used in probability, statistics and time-series analysis.

Here are some examples:

• it is used to compute the autocorrelation function of a process;

• it is used to derive Laws of Large Numbers for correlated sequences.

More details

Other concepts related to covariance stationarity can be found in the lecture on sequences of random variables.

Keep reading the glossary

Previous entry: Covariance formula

Next entry: Critical value

How to cite

Please cite as:

Taboga, Marco (2021). "Covariance stationary", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/covariance-stationary.